1. L’un des grands problèmes de la mathématique grecque fut la quadrature du cercle . Mais ce problème fut attaqué, pour la première fois dans l’histoire des mathématiques, par les géomètres d’Égypte.

Richard J. Gillings n’en pense pas moins : « But his method allows him to find a square nearly equal to a circle, so that we can credit A’hmosè with being the first authentic circle-squarer in recorded history ! » (R.J. Gillings, Mathematics in the time of Pharaohs, New York, Dover Publications, 1982, P. 145 ).

Traduction : « Mais sa méthode lui permet de trouver un carré à peu près égal à un cercle, de sorte que nous pouvons reconnaître que Ahmes passe pour avoir été le premier (géomètre) authentique à inscrire un cercle dans un carré au vu de l’histoire écrite ! ».

A’h-mosé ou Ahmès est le sribe-mathématicien qui a recopié, vers 1650 av. notre ère, le texte mathématique égyptien connu aujourd’hui sous la désignation de « Papyrus de Rhind ». De fait, la méthode de chercher le carré du cercle apparaît, pour la première fois dans l’histoire écrite des mathématiques, avec le problème n° 48 de ce papyrus.

Ainsi, bien après les Égyptiens (vers 1650 av. notre ère), et le géomètre Hippocrate de Chios (Ve siècle av. notre ère), Archimède de Syracuse (vers 287-212 av. notre ère) développe tout un programme de recherche dans la perspective de pouvoir faire la quadrature du cercle .

2. Archimède commence à s’intéresser aux objets dont les grandeurs – longueur, aire, volume – ont quelque chose à voir avec celles du cercle (sphère, cylindre, cône, spirale).

  Dans une deuxième étape, il étudie les figures courbes particulières (paraboles et lunules), dont on peut faire la quadrature.

  Enfin, dans une troisième étape, Archimède propose une méthode de calcul pour approcher la mesure du cercle.

3. A l’époque d’Archimède, le gymnase ne laissait que peu de place aux disciplines scientifiques et à la géométrie. De plus, Syracuse, la ville natale d’Archimède, ne comportait aucune école de niveau supérieur au gymnase.

Il est évident qu’à cette époque, qui voulait devenir savant allait à Alexandrie…en terre africaine d’Égypte.

Comme autrefois Thalès venant de Milet, ou Pythagore de Samos, Archimède a fait le voyage en Égypte, lui venant de Syracuse, vers le milieu du IIIe siècle av. notre ère. Astronomie, médecine, mathématiques et mécanique, étude de la nature, littérature, grammaire, géographie, florissaient alors à Alexandrie. La bibliothèque du Musée d’Alexandrie avait plus de 500 000 papyrus : tout Homère, la bibliothèque entière d’Aristote, les Tragiques (Sophocle, Euripide, Eschyle), les grandes comédies (Aristophane, etc.), Platon, les récits des voyages, les écrits des poètes, de ceux qui avaient dit comment étaient les nombres (Pythagore), les Éléments d’Euclide (treize volumes).

Mais, surtout, l’immense héritage pharaonique était encore directement lisible avec des savants comme le prêtre et historien autochtone du IIIe siècle av. notre ère, le célèbre Manéthon, auteur d’une Histoire d’Égypte aujourd’hui disparue. Les égyptologues, encore de nos jours, ne font que suivre la chronique manéthonienne des dynasties pharaoniques.

Platon et Aristote, en leur temps, ont célébré les inventions astronomiques, mathématiques, artistiques et linguistiques du génie égyptien.

C’est de Conon, géomètre alexandrin, qu’Archimède apprit une courbe étonnante, faisant plusieurs révolutions autour d’un point dont elle s’écarte un peu plus à chaque tour : la spirale.

Archimède n’avait rien écrit avant son départ en Égypte. C’est de retour à Syracuse, des années plus tard, qu’Archimède rédigea ses traités de mathématiques, en ayant d’ailleurs une pensée pour Conon, lui qui eût été en mesure de comprendre ses écrits et de porter sur eux un jugement autorisé.

4. La quadrature du cercle en Égypte. Les faits ci-après le démontre effectivement.

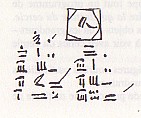
C’est le problème n° 48 du Papyrus Rhind.

Cette figure tracée par le scribe représente un cercle inscrit dans un carré. La valeur du signe à l’intérieur de la figure est 9 : c’est à la fois le côté du carré et le diamètre du cercle. Le côté du carré est égal au diamètre du cercle.

Le scribe calcule la surface du carré : 9 x 9 = 81

Il calcule ensuite la surface du cercle : 8 x 8 = 64

Ce qui s’explique : le carré et le cercle ont le côté et le diamètre dans le rapport 8/9. Leurs surfaces sont approximativement égales. Ce dont le cercle dépasse le carré (la partie hachurée) est à peu près égal à ce dont la carré dépasse le cercle (la partie quadrillée). Ainsi :

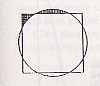
On peut aussi interpréter les données égyptiennes de cette autre manière. Le cercle est assimilé à un octogone irrégulier dont les dimensions sont indiquées sur la figure ci dessous et dont la surface est 63, mais 64 étant préféré à 63 par le scribe parce que c’est un carré parfait. Ainsi :

Figure : Le cercle est assimilé à un octogone irrégulier.

La surface du carré est : 9 x 9 = 81.

Celle des 4 triangles isocèles qui forment ensemble deux petits carrés de côté 3, est égale à :

(3 x 3) x 2 = 18.

La surface du cercle est donc :

81 – 18 = 63

64 étant préféré à 63 parce que c’est un carré parfait.

Au total, les Égyptiens ont comparé le carré et son cercle circonscrit. Ce qui pose le problème de la détermination du rapport du diamètre et du côté. Ils ont vu que le cercle avait une plus grande surface. Ils ont alors cherché le carré qui a une surface à peu près égale à celle du cercle, c’est à dire le carré intermédiaire entre le carré circonscrit et le carré inscrit. Ils ont noté le rapport 8/9 dans lequel se trouvent le côté du carré et le diamètre du cercle.

Une certaine compréhension des rapports géométriques s’impose de toute évidence. Il faut également mettre bien en relief la compréhension de la constance de l’égalité des surfaces des cercles et des carrés dont les diamètres et côtés sont dans le rapport 8/9, et cela quelles que soient les dimensions absolues de ces figures. Cette constance est comparable à la constance de Pi, du rapport entre la surface et le rayon.

Avec ce rapport de 8/9, c’est donc aux Égyptiens que revient, dans l’histoire des mathématiques, la toute première tentative de résolution de la quadrature du cercle.

5. La quadrature du cercle par Archimède.

Avant Archimède et après les Égyptiens, Euclide, au livre XII de ses éléments, a démontré qu’il y a pour tout cercle un rapport constant entre l’aire de ce cercle et l’aire d’un carré dont le côté est le rayon (la moitié du diamètre) du cercle.

C’est dans son traité La mesure du cercle qu’Archimède s’est attaqué à la quadrature du cercle.

Figure : Quadrature du cercle par Archimède.

Bibliographie : Théophile OBENGA, « La Géométrie Égyptienne », Éditions l’Harmattan, Khepera, 1995.

*******

Notes de ETILE René-Louis :

  Pour l’africanité d’Euclide voir le livre du mathématicien français Christian VELPRY, «  Euclide l’Africain  », Éditions MENAIBUC, 2004.

  On a 8 x 8 = 64 et 9 x 9 = 81

La valeur approximative du nombre Pi à Kémèt est 4 fois 64/81 ,

ce qui donne environ 3,16 (au lieu de 3,14…)